A simple guide to Big-O notation

Big-O notation is used in Computer Science to describe the performance or complexity of an algorithm. Big-O notation characterizes functions according to their growth rates: different functions with the same growth rate may be represented using the same O notation.

The letter O is used because the growth rate of a function is also referred to as the order of the function. A description of a function in terms of big O notation usually only provides an upper bound on the growth rate of the function. Associated with big O notation are several related notations, using the symbols o, Ω, ω, and Θ, to describe other kinds of bounds on asymptotic growth rates.

This is the best way to understand Big-O thoroughly to produce some examples:

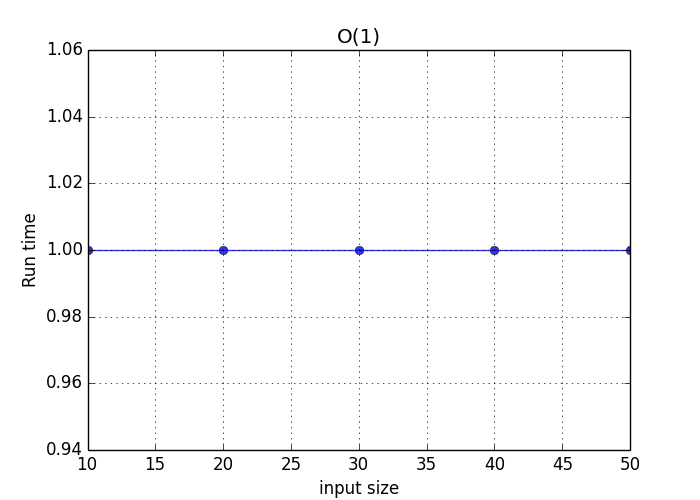
O(1) - Constant time complexity

O(1) describes an algorithm that will always execute in the same time (or space) regardless of the size of the input data set. As the input increases, time to run the algorithm stays constant.

const firstEven = (array) => {
    return array[0] % 2 === 0;
}

Usage:

• determining if a binary number is even or odd,
• constant-size lookup table

O(1) plot:

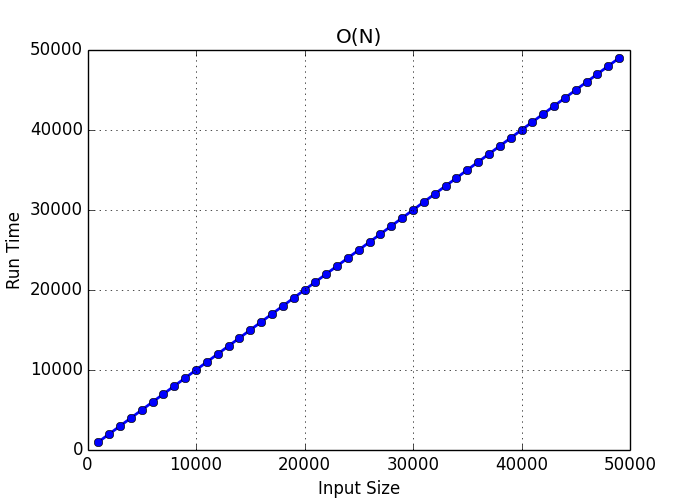
O(n) - Linear time complexity

O(n) describes an algorithm whose performance will grow linearly and in direct proportion to the size of the input data set. As the input increases, the time to run the algorithm will grow proportionally.

const hasValue = (array, value) => {
    for (var i = 0; i < array.length; i++) {
        if (array[i] === value) {
            return true;
        } 
    }
    return false;
}

Usage:

• finding an item in an unsorted list or in an unsorted array,
• adding two n-bit integers by ripple carry.

O(n) plot:

O(2n) - Exponential time complexity

O(2n) denotes an algorithm whose growth doubles with each additon to the input data set. The growth curve of an O(2n) function is exponential - starting off very shallow, then rising meteorically. An example of an O(2n) function is the recursive calculation of Fibonacci numbers:

const fibonaci = (number) => {
    if (number <= 1) {
        return 1;
    }
    return fibonaci(number - 1) + fibonaci(number - 2);
}

Usage:

• finding the (exact) solution to the travelling salesman problem using dynamic programming
• determining if two logical statements are equivalent using brute-force search

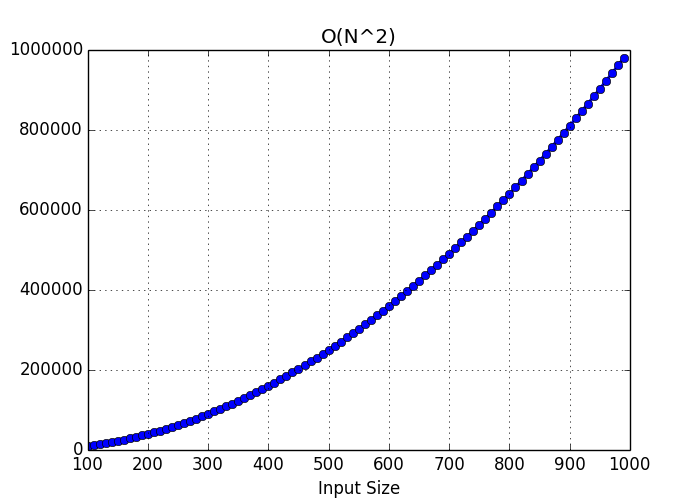
O(n²) - Quadratic time complexity

O(n²) represents an algorithm whose performance is directly proportional to the square of the size of the input data set. This is common with algorithms that involve nested iterations over the data set. As the input increases, the time to run the algorithm grows at the rate of it’s square.

const findMatch = (string) => {
    for (var i = 0; i < string.length; i++) {             /* has O(n) time complexity */
        for ( var j = i + 1; j < string.length; j++) {    /* has O(n2) time complexity */
            if (string[i] === string[j]) {
                return true;
            }
        }
    }
    return false;
}

O(n²) plot:

Deeper nested iterations will result in O(n3), O(n4) etc. This is like O(n²) algorithm, but with 3 loops instead of 2:

const findMatch = (string) => {
    for(var i = 0; i < string.length; i++) {              /* has O(n) time complexity */
        for(var j = i + 1; j < string.length; j++) {      /* has O(n2) time complexity */
            for(var k = j + 1; k < string.length; k++) {  /* has O(n3) time complexity */
                if (string[i] === string[k]) {
                    return true;
                }
            }
        }
    }
    return false;
}

Usage:

• simple sorting algorithms, such as bubble sort, selection sort and insertion sort
• (worst case) bound on some usually faster sorting algorithms such as quicksort, Shellsort, and tree sort

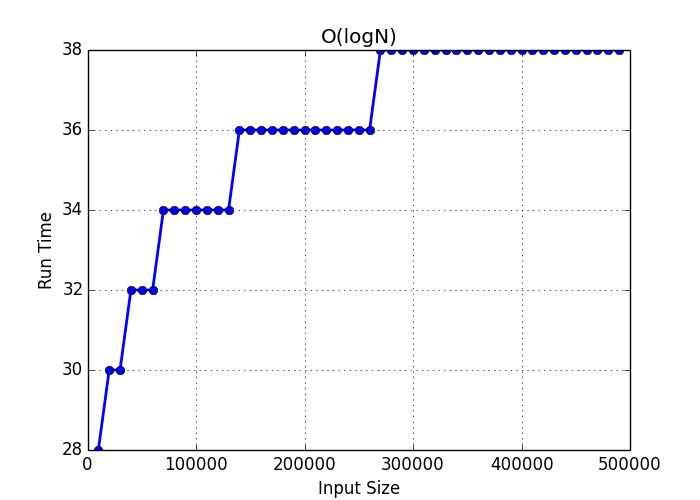
O(log n) - Logarithmic time complexity

O(log N) basically means time goes up linearly while the n goes up exponentially. So if it takes 1 second to compute 10 elements, it will take 2 seconds to compute 100 elements, 3 seconds to compute 1000 elements, and so on.

An example is binary search, which is often used to search data sets:

const search = (array, value) => {
    var minIndex = 0;
    var maxIndex = array.length - 1;
    var currentIndex;
    var currentElement;
    while (minIndex <= maxIndex) {
        currentIndex = (minIndex + maxIndex) / 2 | 0;
        currentElement = array[currentIndex];
        if (currentElement < value) {
            minIndex = currentIndex + 1;
        } else if (currentElement > value) {
            maxIndex = currentIndex - 1;
        } else {
            return currentIndex;
        }
    }
    // not found
    return -1;  
}

Usage in finding an item in a sorted array with a:

• binary search
• balanced search tree as well as all operations in a Binomial heap

O(log n) plot:

O(n log n) - Logarithmic time complexity

For each input, the algorithm is running an operation at O(log n)

for (var i = 1; i < n; i = i * 2) {
    for (j = n; j >= 1; j = j/2) {
        console.log(j);
    }
}

Usage:

• performing a fast Fourier transform,
• fastest possible comparison sort,
• heapsort
• merge sort

Big-O Complexity Chart

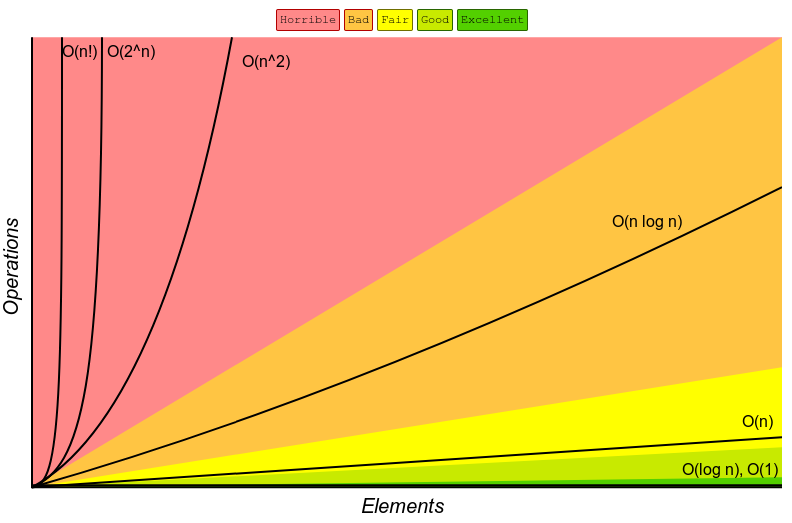
Keep in mind that Big O notation is just an estimation so it’s not meant to be an exact calculation.